前言
之前一直有整理几年来所看所学的深度学习 / 机器学习知识的想法，但是总会因为各种各样的原因耽搁，这次借着面试前的准备，以四大生成模型为目标，从头把这些知识梳理一下。
前馈神经网络（Forward Neural Network, FNN）
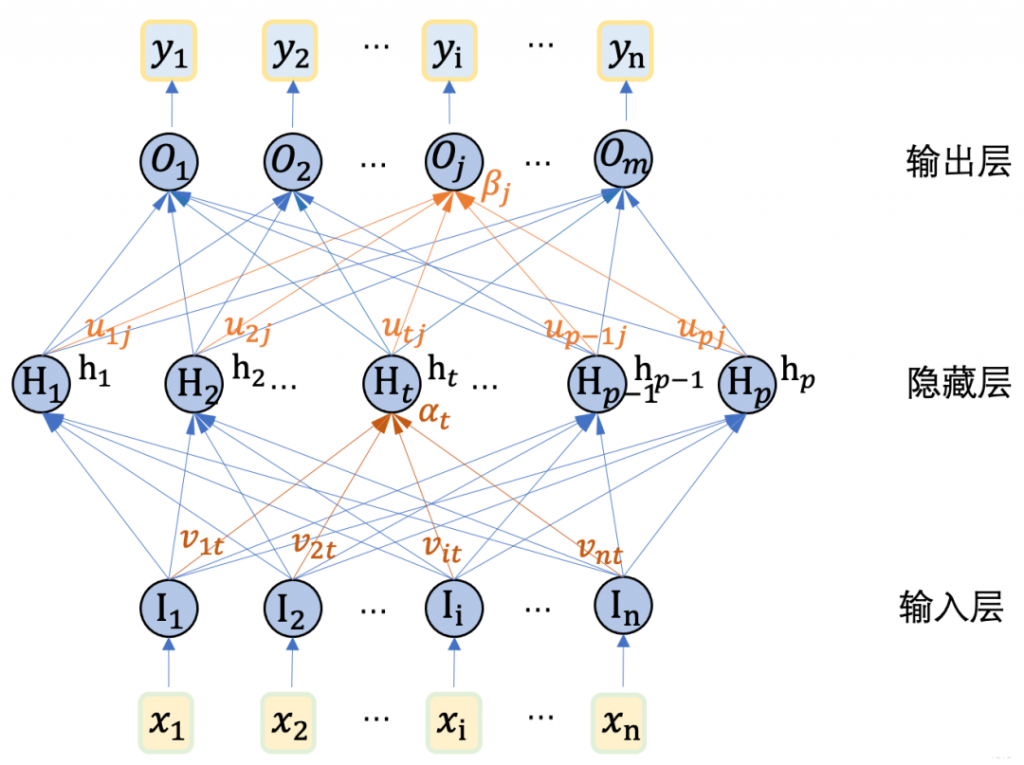
FNN 是最基础的神经网络模型。由输入层、若干隐藏层和输出层组成。隐藏层里有若干个神经元，将输入进行“加工”，最终得到输出。
多层感知机（Multilayer Perceptron, MLP）
每个神经元与前后层的所有神经元都相连（全连接），可以说由若干个全连接层堆叠而成，但是多层感知机的隐藏层里面，还有激活函数（非线性变换）。
想象你要做一道多步骤的手工艺品：
- 拿到原料（输入），
- 经过第一个工序（第一层神经元）做简单加工，
- 得到半成品，再交给第二个工序（第二层神经元），
- 如此依次推进，直到最后一步拿到成品（输出）。
在这个“流水线”里，原料永远只往前流，不会回头修改；每道工序只关心它收到的半成品如何变得更好。前馈神经网络就是这样一个没有反馈、不形成循环的多层“加工”结构。
（由 GPT-o4 给出解释）
激活函数
激活函数就相当于对这一层神经元的输出做一次非线性的变换。
激活函数就像神经元里的“开关”或“阀门”：当一个神经元收到信号（即上一层的加权和）时，激活函数决定它“放行”多少信号到下一层。没有激活函数，神经网络里所有的层都只是简单地叠加和缩放信号——就像把多块透明玻璃叠在一起，光线依然是直线，网络就只能表示线性关系；有了激活函数，信号可以被“扭曲”或“截断”，网络才具备表达各种复杂、非线性的能力。
（由 GPT-o4 给出解释）
激活函数的作用？也可以说为什么要引入非线性变换？引入非线性变换之后为什么模型的表达能力就变强了？
如果没有激活函数，输入就相当于在和一堆矩阵做相乘运算，乘来乘去总是线性的变换（要不然为啥矩阵要叫做线性代数），可以想象成对一个变量 x 反复地乘上一些数字（x→ax），加再多层都和只用一层一样。
还有一个原因，将特征进行非线性映射的另一个用处，可以让输出满足下游任务的要求，将输出的值限制在一定的范围内（特征空间），也能提升模型的性能。
常见的激活函数
| 名称 | 表达式 | 特点 |
| Sigmoid | $$\sigma (x) = \frac {1} {1+e^{-x}}$$ | 输出范围 (0,1)，适合二分类；易饱和，梯度消失问题 |
| Tanh | $$\tanh (x) = \frac {e^{x}-e^{-x}} {e^{x}+e^{-x}}$$ | 输出范围 (−1,1)，中心对称；同样存在梯度消失 |
| ReLU | $$\max (0,x)$$ | 计算简单，稀疏激活，收敛快；负区间恒为0，可能导致神经元死亡 |
| LeakyReLU | $$\max (\alpha x,x), \alpha \in (0, 1)$$ | 对负区间保留小斜率，解决 ReLU 死神经元 |
| ELU | \(x>0时：x\) \(x \le 0时：\alpha (e^{x}-1)\) | 负区间平滑、输出均值更接近零，收敛更稳定 |
| Softmax | $$\frac {e^{x_i}} {\Sigma_{j}e^{x_j}}$$ | 将向量映射为概率分布，多分类输出常用 |
| GELU | $$x\Phi (x) $$ | Transformer 中常用，平滑又具备自正则化特性 |
| Swish | $$x\sigma (x) $$ | 比 ReLU 更平滑，实验证明性能略优 |
损失函数（Loss Function）
模型在完成加工后会得到一份输出 \( \hat y \) ，用该输出和真实的标签进行误差的计算，我们希望模型的输出和真实标签之间越接近越好，所以神经网络训练时，会尽可能让损失函数的值小，一般求出整个训练集的损失再求期望，然后最小化这个值。
损失函数就像考试中的“分数”，用来衡量模型的“答题”结果（预测）跟“正确答案”之间差了多少。分数越低，说明模型表现越好；分数越高，说明模型和你期望的结果差距越大。训练神经网络的过程，就是不停地“批改考试卷”——根据损失分数调整模型参数，让它下一次答题时更接近满分。
（由 GPT-o4 给出解释）
如何最小化？通过反向传播计算梯度，再用诸如梯度下降的方法去优化参数。
反向传播（Backpropagation, BP）
根据得到的损失值，回过头去计算各个神经元的误差。通过损失计算每层参数的梯度，再利用梯度下降等优化方法更新神经元的权重和偏置参数。
由损失值 \( \mathcal{L} \) 计算参数 \( \omega \) 的梯度涉及导数的链式法则，比如第 \( z – 1 \) 个神经元的参数 \( \omega_{z-1} \)，先影响到第 \( z \) 个输出层神经元的输入 \( \beta \)，再影响到其输出值 \( \hat y \) ，最后影响到损失函数值，这个过程有：
$$ \frac {\partial \mathcal {L} } {\partial \omega_{z – 1}} = \frac {\partial \mathcal {L} } {\partial \hat {y}} \cdot \frac {\partial \hat {y}} {\partial \beta} \cdot \frac {\partial \beta} {\partial \omega_{z}} $$
（来自周志华的《机器学习》一著。回顾这部分时仍然花了很多时间才理解）
求得梯度后，按梯度的反方向在给定的学习率下对参数进行更新：\( \theta \gets \theta – \nabla \theta \)。而不同的更新方式又涉及到不同的优化算法。
优化器（Optimizer）
随机梯度下降（Stochastic Gradient Descent, SGD）
最基本的优化器，更新参数时每次只用一小批样本计算梯度：
$$ \theta \gets \theta – \eta \nabla_{\theta} $$
经典而简单，但容易卡在梯度较小的点或局部最优点。
带动量的 SGD（SGD with Momentum, SGDM）
当前梯度方向能由过往的方向和当前梯度共同决定：
$$ \begin{align} \theta &\gets \theta – v, \\ v &\gets \alpha v + \eta \nabla_{\theta} \end{align} $$
相当于为参数加上了“惯性”，在遇到下坡时，提升收敛速度；遇到低谷时，模型也会尝试再往前走一点，平滑更新+加速收敛。（不过额外引入了动量系数，多一个参数需要调）
自适应梯度下降（AdaGrad 和 RMSProp）
AdaGrad 优化算法就是在每次使用一个 batch size 的数据进行参数更新的时候，算法计算所有参数的梯度，那么其想法就是对于每个参数，初始化一个变量 s 为 0，然后每次将该参数的梯度平方求和累加到这个变量 s 上，然后在更新这个参数的时候，学习率就变为：
$$ \frac {\eta} {\sqrt{s + \epsilon}} $$
\(\epsilon\) 是一个极小的正数，防止分母为 0 用的。如果一个参数的梯度一直都非常大，那么其对应的学习率就变小一点，防止震荡，而一个参数的梯度一直都非常小，那么这个参数的学习率就变大一点，使得其能够更快地更新。（但是这个时候又会导致学习率衰减过快，训练后期几乎停止）
（上述部分参考自：【快速理解Adagrad】通俗解释Adagrad梯度下降算法-CSDN博客）
RMSProp 在 AdaGrad 的基础上又做了进一步修改，得到最新的梯度后并不是直接平方后加到原来的 s 上，而是和原来的 s 进行加权求和。假设最新求得的梯度为 \(g_t\)，s 的更新方式就变为：
$$ s_{t} = \beta s_{t-1} + (1-\beta) g_{t}^{2} $$
其他还是和 AdaGrad 一致。这样就能在自适应调节学习率的基础上，保持长期与近期梯度信息的平衡，适应性更佳。但引入新的超参数 \(\beta\) 又让调参的难度上升。（默认取 0.9）
Adam 与 AdamW
Adam 结合了 SGDM 和 RMSProp 的优势，既引入了动量，又引入了自适应更新。首先是引入了动量，其梯度更新（不是学习率）变成了这样：
$$ \frac {\eta} {\sqrt{\hat{v}_{t} + \epsilon}} \hat{m}_{t} $$
其中的 \(\hat{v}_{t}\) 和 \(\hat{m}_{t}\) 都会随着训练而自行调整。先看不带帽子的 \({v}_{t}\) 和 \({m}_{t}\) ：
$$ \begin{align} v_t &= \beta_1 m_{t-1} + (1-\beta_1) g_{t}^{2}, \\ m_t &= \beta_2 m_{t-1} + (1-\beta_2) g_t \end{align} $$
这里需要注意，\(g_{t}\) 是带 L2 正则化的梯度，会在损失函数里加上 \(\frac{\lambda}{2}\left | \theta \right |^2\) ，然后导致 \(g_{t}\) 里多一项 \( \lambda\theta \)：
$$ g_t = \nabla_{\theta} + \lambda \theta $$
其他地方 \({v}_{t}\) 还是和 RMSProp 一样，而 \({m}_{t}\) 没有对梯度求平方，直接加权求和了。（\( \beta_{1} \) 默认为 0.9，\( \beta_{2} \) 默认为 0.999）
但这两个值在训练初期会往 0 靠近，所以又给 \({v}_{t}\) 和 \({m}_{t}\) 做偏差校正：
$$ \begin{align}\hat{v}_{t} &= \frac {v_t} {1-\beta_{1}^{t}}, \\ \hat{m}_{t} &= \frac {m_t} {1-\beta_{2}^{t}}\end{align} $$
分母的 \( \beta_{*}^{t} \) 是对超参数求 t 次方。这样在训练初期的学习率就上去了，而训练后期学习率减少，允许模型做细致的探索。
AdamW 的思路很简单，把加在 \(g_{t}\) 上的权重拿出来，改为直接加在最后的权重更新步骤上，这时候的 \(g_{t}\) 就是 \(\nabla_{\theta}\)，然后求 \({v}_{t}\) 和 \({m}_{t}\)（加个权 α），最后再进行权重衰减：
$$ \theta_t \gets \theta_{t-1} – \eta \left( \alpha \frac {1} {\sqrt{\hat{v}_{t} + \epsilon}} \hat{m}_{t} + \lambda \theta_{t-1} \right) $$
原来 Adam 中 λ 会同时影响衰减和自适应计算，但 AdamW 只影响最后的衰减步骤，不会干扰梯度的自适应比例计算。（看了半天 AdamW 觉得懵懵懂懂的。。。复杂但好用）
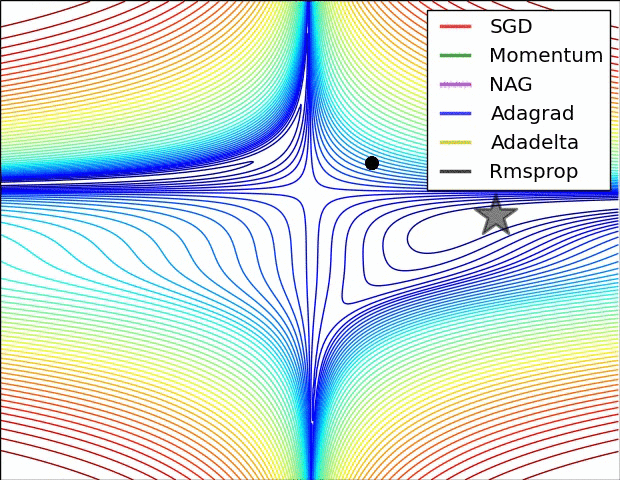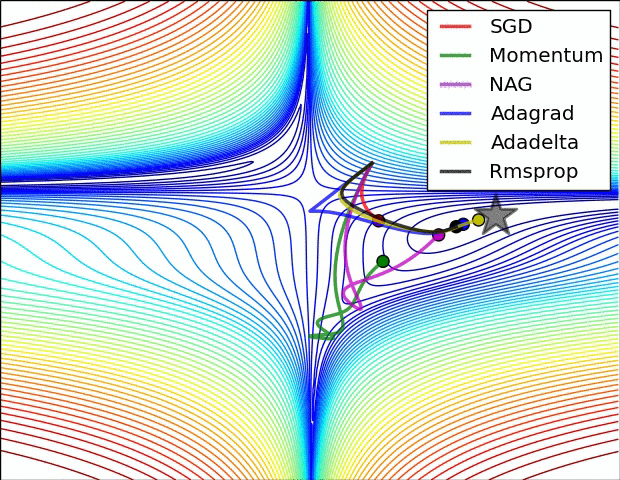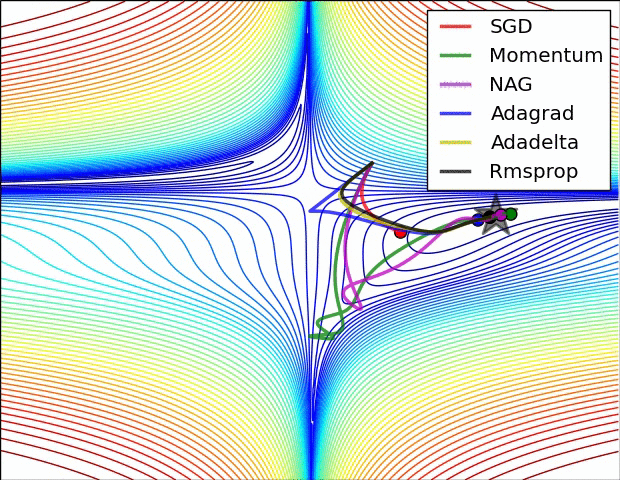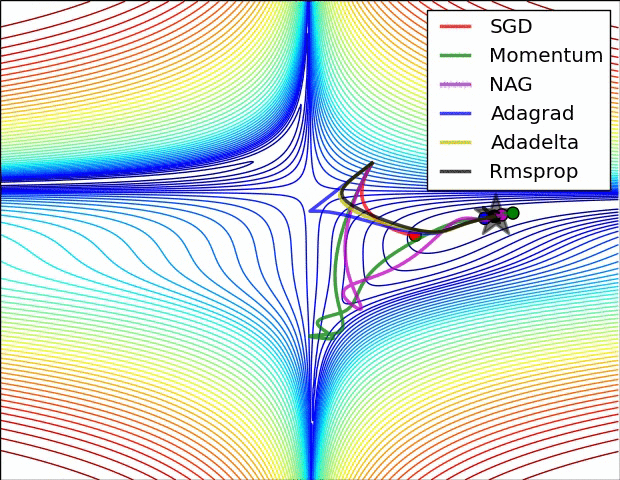
关于不同优化器的可视化比较（NAG 和 Momentum 类似，Adadelta 和 RMSProp 类似）：
正则化技巧
Dropout
简单地说就是让模型在训练时随机让一部分神经元“休息”，强迫所有神经元都掌握到知识。
说是休息，实际上只是这些神经元的输出被屏蔽掉了（神经元：我上早八）。
对每一层的激活后的输出加一个服从伯努利分布的随机掩码，以概率 p 让神经元的输出为 0，然后对剩下有效的输出除以 (1 – p) 保持期望一致（不然整体期望会变小）
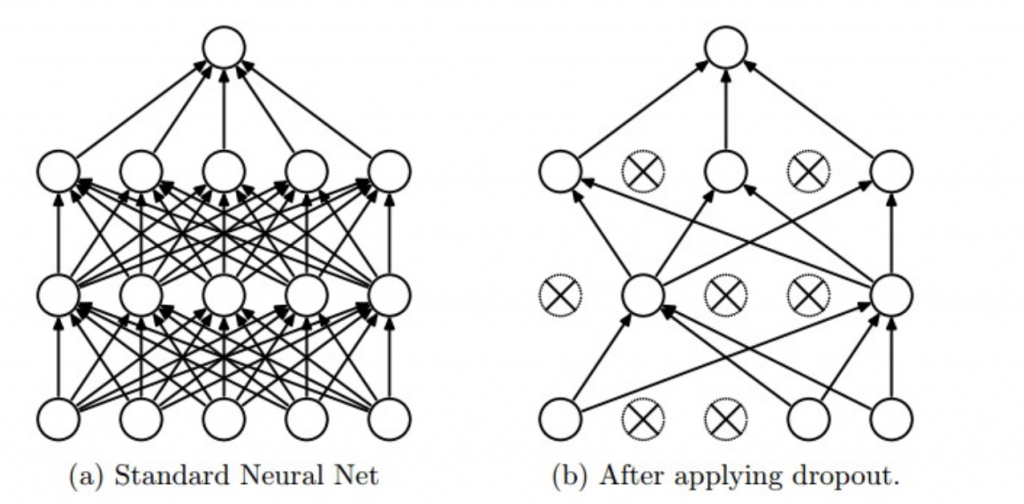
加 Dropout 的目的就是防止过拟合，提升模型的泛化能力，让模型学到更分散的信息表示，不会把所有重任压在少数神经元上。默认的 Dropout 率是 0.3~0.5，输入层要更低一些，输出层不要做 Dropout。
Dropout也不是万能的，在 BatchNorm 的后面使用 Dropout 需要谨慎考虑，对输出用两种正则化真的会提升性能吗？
对于序列敏感型的模型（如 Transformer）随机屏蔽神经元也有可能破坏掉时序信息。
而且Dropout 会减慢模型的收敛速度，这个也需要考虑。
权重衰减（Weight Decay）
在原来的损失基础上增加一个 L2 正则化项，反向传播的时候梯度后面就会加一项 \( \lambda \theta \)，最后会影响参数的更新：
$$ \theta \gets \theta – \eta(\nabla_\theta + \lambda \theta) = (1-\eta\lambda)\theta – \eta\nabla_theta $$
可以看到相当于对原来的参数按比例进行收缩，把那些很大的权重往回拉一些，减少极端权重带来的不稳定梯度，也是一种正则化策略。
批归一化（BatchNorm）和层归一化（LayerNorm）
归一化，即减均值再除以方差，但是 BatchNorm 和 LayerNorm 求均值和方差的方式不一样，BatchNorm 针对的是这一批特征张量的每个通道，LayerNorm 针对的是这一批特征张量的每个特征，看下面这张图片：
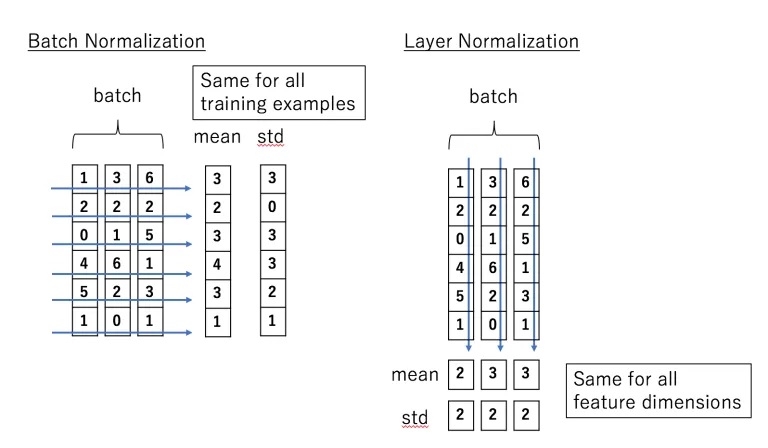
公式不列了，BatchNorm 和 LayerNorm 各有各的优点和适用范围。
因为 BatchNorm 是对所有特征的同一个通道做归一化，所以会抹掉不同特征之间的大小关系。
（想象班上考了五次试，最高分分别是100，90，80，70，60，然后老师分别把每次考试所有学生的分数求归一化，这个时候这五次考试的最高分之间并没有什么可比性，都是 1 了）
如果模型的任务对特征间的大小关系没有特别的依赖（数据没有时序关联），就可以使用 BatchNorm，比如图像分类、目标检测、语义分割。而且 BatchNorm 的执行效率更高，适合大 Batch 训练。但是 Batch 很小的时候会导致 BatchNorm 不稳定，而 LayerNorm 就更合适。
再看到 LayerNorm，因为它是对每条特征做归一化，所以就保留了不同特征间的大小关系。
（还是想象班上考了五次试，这次老师把每个学生的五次考试分数分别进行了归一化，这个时候这五次考试的最高分就有区别了，因为可能被放在不同的学生身上并归一化，并不都是 1 了）
LayerNorm 适合变长序列和小 Batch 训练，能保持序列内部不同位置间的大小关系，可以用在需要处理语音、文本流的模型，比如注意力模型、Transformer。